逐点比较法直线插补为例说明插补的具体过程。

1．插补原理

逐点比较法又称区域判断法或代数运算法、醉步法。其基本原理是：每走一步都要将加工点的瞬时坐标与规定的图形轨迹相比较，判断一下偏差，然后决定下一步的走向。这种方法的特点是：运算直观，插补误差小于一个脉冲当量，输出脉冲均匀，而且输出脉冲的速度变化小，调节方便，因此，在两坐标联动的数控机床中应用较为广泛。

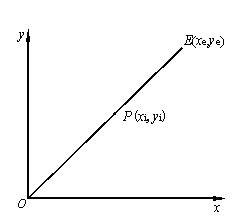
图2-6 逐点比较法直线插补

 

如图2-6所示，第Ⅰ象限直线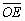的起点为坐标原点，终点为E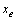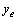（，），加工动点为（，）。

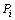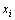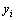（1）偏差判别  由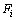的数值可以判别动点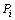与直线的相对位置。

（2）坐标进给

（3）新偏差计算

由此可知，新加工点的偏差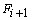完全可以用前加工点的偏差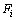递推出来，偏差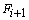的计算只作加法和减法运算，没有乘法运算，计算简单。

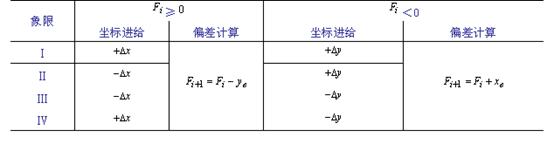
其它象限直线的插补偏差递推公式可同理推导。四个象限的直线插补偏差计算递推公式如表2-1所示。

 

表2-1  直线插补公式

（4）终点判断

2．插补实例

【例题2-1】设加工第Ⅰ象限直线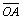，起点坐标为O（0，0），终点坐标为A（6，4），试进行插补运算并画出运动轨迹图。

用第一种方法进行终点判断，则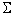=6＋4=10，其插补运算过程见表2-2，插补轨迹如图2-7所示。

 

表2-2  逐点比较法直线插补运算表

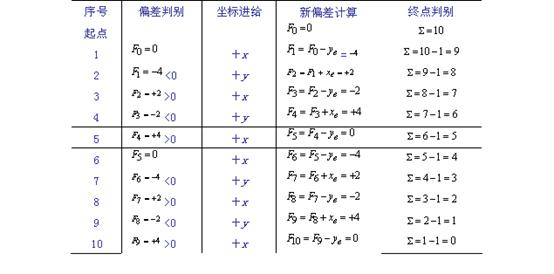
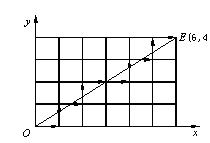
图2-7 直线插补运动轨迹图