确定最短的走刀路线，除了依靠大量的实践经验外，还应善于分析，必要时辅以一些简单计算。现将实践中的部分设计方法或思路介绍如下。

①巧用对刀点 图1(a)为采用矩形循环方式进行粗车的一般情况示例。其起刀点A的设定是考虑到精车等加工过程中需方便地换刀，故设置在离坯料较远的位置处，同时将起刀点与其对刀点重合在一起，按三刀粗车的走刀路线安排如下：

第一刀为 A→B→C→D→A

第二刀为 A→E→F→G→A 

第三刀为 A→H→I→J→A

图1(b)则是巧将起刀点与对刀点分离，并设于图示B点位置，仍按相同的切削用量进行三刀粗车，其走刀路线安排如下：起刀点与对刀点分离的空行程为A→B

第一刀为 B→C→D→E→B

第二刀为 B→F→G→H→B

第三刀为 B→I→J→K→B

显然，图1(b)所示的走刀路线短。

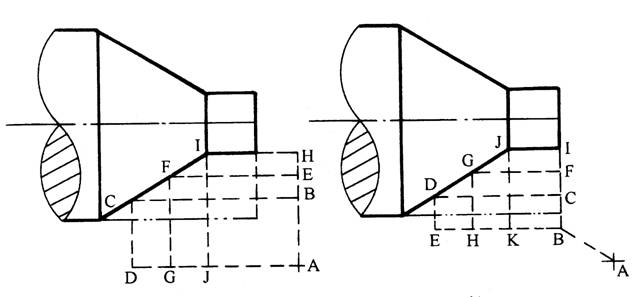
(a) 起刀点对刀点重合                                     (b) 起刀点对刀点分离

图1  巧用起刀点

②巧设换刀点  为了考虑换（转）刀的方便和安全，有时将换（转）刀点也设置在离坯件较远的位置处（如图1中A点），那么，当换第二把刀后，进行精车时的空行程路线必然也较长；如果将第二把刀的换刀点也设置在图1(b)中的B点位置上，则可缩短空行程距离。

③合理安排“回零”路线  在手工编制较复杂轮廓的加工程序时，为使其计算过程尽量简化，既不易出错，又便于校核，编程者（特别是初学者）有时将每一刀加工完后的刀具终点通过执行“回零”（即返回对刀点）指令，使其全都返回到对刀点位置，然后再进行后续程序。这样会增加走刀路线的距离，从而大大降低生产效率。因此，在合理安排“回零”路线时，应使其前一刀终点与后一刀起点间的距离尽量减短，或者为零，即可满足走刀路线为最短的要求。